A Conceptual Guide to Transformers: Part I
Architecture of the Transformer Model
Rest of the series: Part II (second post on the architecture with clarifications and cleanup), Part III (Mechanics of Training), Part IV (How to Think about LLMs), Part V (What’s Going on Under the Hood)
Everybody has been chattering about chatGPT and other Large Language Models lately. If you’re like me, you’ve found AI’s new-found ability to generate fairly cogent and very fluent text to be almost magical. These LLMs are all transformer models, and transformers are often presented in a less-than-comprehensible way, especially to those who aren’t highly familiar with other natural language processing (NLP) paradigms in machine learning.
My main goal in this sequence of posts is to provide a conceptual guide to transformers. Transformers have a lot of moving parts, and so in this first post, I’m going to provide an initial walkthrough that makes a number of simplifying assumptions so you don’t have to keep too much nuance in your head to begin with. In the second post, I’ll talk more about the various parts of the architecture and remove some of the simplifications made in this post.
Later posts will discuss training, scaling, and other conceptual issues related to transformers that I find interesting.
Ideally, at least 90% of this first post should be comprehensible to someone who doesn’t know what a vector is and has never coded before. I hope at least 95% is comprehensible if you’ve at least seen matrix multiplication at some point in your life.
Some Caveats
First, unlike most other presentations I see, I will focus on conceptual understanding to the near exclusion of very important implementation details. This won’t in any way be a guide to coding up your own transformer. However, it’s likely I will also unintentionally say some false things, so I will try to flag where I’m skipping or fudging details so adept readers can distinguish white lies from mistakes.
Second, I make no claim to originality at any point. I’m heavily indebted to a number of sources, but especially to this Anthropic paper and to Neel Nanda’s youtube videos on transformers. If you’re interested in learning more, I highly recommend the linked content.
Basic Overview
We’re going to be talking about decoder-only transformers, which is what ChatGPT and other GPT-series models are based on. The original Vaswani et al. (2017) paper that introduced transformers presented an encoder-decoder architecture, which is more complicated but also more geared to tasks like translation. I also found the original paper and the diagrams pretty hard to read at first, and I think a lot of subsequent explainers are much better at presentation.
You can think about transformer models as producing a probability distribution over all potential next words given an input string of text. For instance, consider the string The world is the totality of. Our transformer will produce a probability over all next words in the vocabulary to continue. So, it will produce a probability that the next word is facts, but also a probability that the next word is elephant.
We can generate longer completions by having it then select a word and then adding it to the initial sequence and continuing on. (We could have it take the likeliest word or select words randomly weighted by the probability it assigns or use some other method.) So, suppose it selects facts as the next word. We then feed The world is the totality of facts into the model and get a new probability distribution over the vocabulary and continue on.
Brief mention of the most important fudges here: (1) What the model really sees is tokens and not words, where tokens are something like sub-words, punctuation, and other useful features of the text. It likewise generates a probabilities over tokens. I will almost completely ignore this wrinkle later, but I’ll generally use the term ‘token’, and you may as well think of it as basically synonymous with ‘word’. (2) The model actually will produce a probability distribution for the next word (token) given every initial subsequence. So, it will assign a probability that the next word after The is elephant, that the next word after The world is elephant, that the next word after The world is is elephant, etc.
Main Components
In this section, I want to zoom in just a bit to get a sense of the main components of the architecture. Unfortunately, there is a tradeoff when it comes to picking good examples of text to illustrate how the model works. Shorter passages are easier to manipulate, but longer passages are more useful for displaying the power of the transformer model. So, I’ll use some examples of each as we go.
Let’s start with a longer passage, which I’ll call Russ.
I have heard of a touchy owner of a yacht to whom a guest, on first seeing it, remarked, “I thought your yacht was larger than it is,” and the owner replied, “No, my yacht is not larger than it is.”
This string is 41 words long. I’ll use Russ[n] to denote the nth word in the sequence. So Russ[3] is heard. I’ll use Russ[:n] to denote the sequence up to and including the nth word. So Russ[:5] is I have heard of a. Here’s what happens in the model:
Take some initial text, such as Russ[:21] (up to the word
thoughtin the first quotation).Change each word into a vector. For now, think of the vector for a word just as a list of numbers that contains information about the word and also its position in the text. At this point, there’s no information encoded about surrounding words. E.g., Russ[12] is
whom, and the vector for Russ[12] does not yet tell the model thatwhomanaphorically refers to the yacht owner, but it does tell the model that this vector is for the word in the 12th position. (This is called the embedding.)Now there’s a list of vectors—i.e., a matrix, or if you prefer, a tensor—with one vector for each word. Somehow or other, the model will have to figure out how the words (now encoded as vectors) relate to one another. E.g., the model needs to figure out that Russ[12] has something to do with the yacht owner. So, we run the set of vectors through a number of ‘attention heads’. For a given word in the text, an attention-head will do two things. (i) It determines what other words in the text to pay attention to and how much attention to pay. (ii) It then copies information connected with those words over to the target word. (This was the big innovation involved with transformers.) For instance, it might take the vector for Russ[12] and then add some information it got from the vector for Russ[7] (the first occurrence of
owner). It probably won’t add much information from information related to Russ[3] (heard), which isn’t especially relevant to Russ[12]. In other words, each vector is now slightly massaged by adding on some contextual information it gets from other vectors.Run each massaged vector corresponding to the words in the text through something called a multi-layer perceptron (MLP). At this step, each vector is again treated in isolation without any information being processed from other surrounding vectors.1
Repeat steps 3-4 a bunch. Each attention head block and MLP block combo is called a layer.2
For every vector in the list, make a prediction about the next word. I.e., generate a probability distribution for Russ[n+1] given an input of Russ[:n]) over all words in the vocab. (This is called the unembedding.) This will allow you to select a candidate for the next word in the sequence. And you can keep generating more and more text by feeding the model the actual candidate that was selected.
Russ is a bit complex to work with, so when we dive in deeper, we’ll use smaller sentences. I’ll use a few different examples, but I’ll focus primarily on a running worked example with the minimal-length string I could think of that might be at all interesting, namely:
Amy saw Will
Here’s a high-level view of the process just laid out with a single layer model.
The Embedding
Ok, the attention stuff is the Big New Thing we get with transformers. But especially for people without a lot of background in ML and NLP, it’s important to get a sense of how much information you get from the initial embedding that transforms the words in input text into vectors that get fed through the attention heads.
Let’s say the vocab list is 50,000 words. We can initially represent each word based on where it falls in alphabetical order. A has position 1, aardvark has position 2, zyzzyva has position 50,000, and according to Merriam-Webster, limpidness is right in the middle, so we’ll say it has position 25,000. We can represent these as vectors easily: each word is connected to a 50,000-long list with 1 corresponding to its position and 0 everywhere else. So, aardvark gets [0 1 0 0 0 … 0], etc. These are called one-hot vectors.
Toy Model: One Hot Encoding
Let’s pair this down for Amy saw Will. We’ll take there to be only a six-word vocabulary in our language that the model will make predictions over:
Vocabulary: Amy, Arnett, Be, Saw, Will, Yesterday
So, we can implement our one-hot encoding as follows:
Initial Embedding
This initial one-hot embedding corresponds perfectly with the vocab list, but it doesn’t contain much useful information. Although apples and oranges are similar in important ways, there’s no way of telling from their one-hot embeddings that they have anything to do with one another.
So how do we get this kind of information encoded? As a first approximation, we might come up with a list of traits we could associate with each word in our vocab and give it a score. One trait might be something like ‘fruitiness’, and both apple and oranges would get a high score.
Another (which I bring up for an important historical example we’ll get to below) could be male-genderedness. Words like he, man, boy, and king get high scores on this trait, and words like she, woman, girl, and queen get low scores on this trait. To make things easy, we could give each word a score between -1 and 1 with -1 meaning something like ‘has the exact opposite of that trait,’ 1 meaning ‘perfectly has that trait,’ and 0 meaning ‘has nothing to do with that trait’. If we came up with a long list of these traits and also gave each word in our vocab a score for each of these traits, then we’d get a lot of information about important relationships between different words.
Think of it like this. You have an Excel file, with each row corresponding to one word in your vocab. The columns are the traits [fruitiness, male-genderedness, edibility, footwear-iness, farm-animalness, redness,…]. When two words get similar scores for a column, you know they bear some kind of similarity. Likewise, when they get opposite scores, you know they have some dissimilarity. You can evaluate their ‘overall’ similarity based on how close they are across the whole set. Couch and sofa, for instance, should be about the same along each dimension.
But we can do more than just check for similarity based on how close together the vectors for various words are. We can also do some basic arithmetical operations on these words.
Let’s take two 3 dimensional vectors a = [1, 2, 3] and b = [4, 5, 6]. I can add a to b by just adding each component. So a + b = [1+4, 2+5, 3+6] = [5, 7, 9]. I can likewise determine a-b = [-3, -3, -3]. What if we try this with our embeddings?
We’ll use the historical example: king - man + woman. If the embedding is good, we’ll get the vector queen. Put differently, this sort of embedding can allow the model to understand certain types of analogies like king : man :: queen : woman, rectangle : square :: rectangular prism : cube, etc.3
Another important thing to notice is that by turning words into these vectors, we encode predictively useful information for the model. Although we haven’t yet talked about training, it’s not too hard to see at this stage how this might work. If you embed pineapple, grape, and orange in the right way, and the model has already seen a passage about pineapple juice and grape juice, it can get clued in after seeing orange that the word juice might be on the horizon as the embeddings for all three words will be similar along some important dimensions. This is an instance of transfer learning, where the model can make predictions for words and patterns based on distinct but related words and patterns.
Now, this was very much just a first approximation to how embeddings work. I will explain what’s wrong with what I just presented in the next post. For now, I think it’s good just to think about things as if there were a handcrafted list of human understandable features, and every word gets a score for each feature.
One other thing: We also have to encode the position of words. So we need to know, in our toy example, that Amy is the first word, saw is the second, and Will is the third. We add that into the encoding, and it’s kludgy and conceptually boring. So I’ll mostly just gloss over this and won’t go into the details.
In a model called GPT-3 Small, there are 768 dimensions for the embedding. In fullscale GPT-3, there are 12,288 dimensions for the embedding. Here and below, I’ll use the specs from GPT-3 Small’s architecture, so I’ll generally refer to 768-dimensional vectors associated with each word when I’m talking about a serious model, but we’ll really pair things down for the toy version.
Toy Model: Initial Embedding
Sticking with our simplifications of embedding as containing a list of features initially with numbers between -1 and 1, let’s just come up with 4 features for the toy model:
Features: Future, Tool, Fame, Male
The idea is that each word in the vocabulary initially gets four scores based on how much it has to do with the future, whether it’s tool-like, whether it has to do with fame or famous people, and how much it relates to male-genderedness.
Here is the Initial Embedding:
There’s a lot wrong with this embedding, but it shows why I could think of this as something like the minimally interesting string for a transformer. Saw could be a tool or a past-tense verb. Will is both a name that’s usually for men, a document for estates, a verb, and a future modal. (I’m assuming our toy model doesn’t know about capitalization.)
Unembedding
At the very end of the model, we unembed each word’s vector. At the unembedding, we get probabilities for the next word after every initial subsequence. So, we could cut out all the stuff about attention layers and MLPs and just unembed right after the initial embedding and get predictions.
I don’t want to get into the technicals at all on this just yet, but if we unembedded our toy example, we’d get probabilities that the word after Will is Amy, Arnett, Be, Saw, Will, and Yesterday.
The best the model could do at this point was make its predictions based on information it has about Will alone. It wouldn’t know that Amy saw came before it. It would make the same predictions for the next word after Amy saw Will as it would for Amy will. So it would assign a high probability to be because you often see the word be follow Will. However, after the string Amy saw Will, you’re relatively unlikely to see Be next. So, we need some architecture that allows the model to pick up on contextual information about the whole sequence.
Summary of Embedding
There was a lot here, so let’s sum up the (unrealistic and uncorrected) way embedding works. (See Part II for a more realistic version.)
We take a word in our text and somehow embed as a relatively high-dimensional vector that encodes important information about the word but that does not contain any contextual information about the other words found in the text. Importantly, we also encode information about the word’s position in the text. How that is done is boring and not conceptually important.
Attention Heads
The main architectural innovation of transformers was the introduction of attention heads. This is where the greatest magic happens.
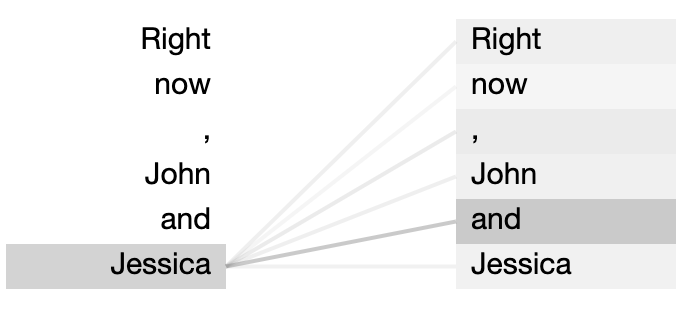
The basic idea is to move information from one part of the text to a later part of the text. Obviously, we need some way to do this to generate fluent and coherent passages. Suppose you feed the model Right now, John and Jessica but don’t have any way to move information from one word to the next. As we just saw, the model will make its prediction for the next token based on the initial embedding of Jessica, so it won’t realize that a present tense verb is much more likely to come next than a past tense one, nor that a plural verb is much more likely than a singular one. What attention will ultimately be able to do is allow the embedding for Jessica to receive information the words preceding it so that, upon unembedding, are is much more likely than it was based on the initial embedding.
The ability to move information from earlier parts of the text to later parts becomes more and more important as the text grows in size. As we saw with the Russ string above, we need to handle anaphora appropriately. If you’re telling a story, you need information about characters and events to be moveable across the string.
The attention heads are the only part of the transformer model that allows for information to be moved from token to token.
I think the best way to get a feel for what attention heads do is with a worked example, which we’ll get to in a second.
But first, I want to emphasize that in the real model, we’ll use a lot of different attention heads. In GPT-3 Small, at every layer, there are 12 different heads (and 144 in total throughout the model). In full-scale GPT-3, there are 96 different heads at each layer (and 9,212 throughout the model). This presumably allows each head to focus on different things. For instance, one head may primarily be trying to figure out what tense of verb is needed, another may try to figure out subject/verb agreement, another may simply look one word back.
How this ultimately works out will depend on what the model decides to do after it’s trained, so don’t take this too literally. We’ll look a bit more in Part V at some stuff attention heads actually do, but here are some graphics showing some attention patterns for GPT-2.
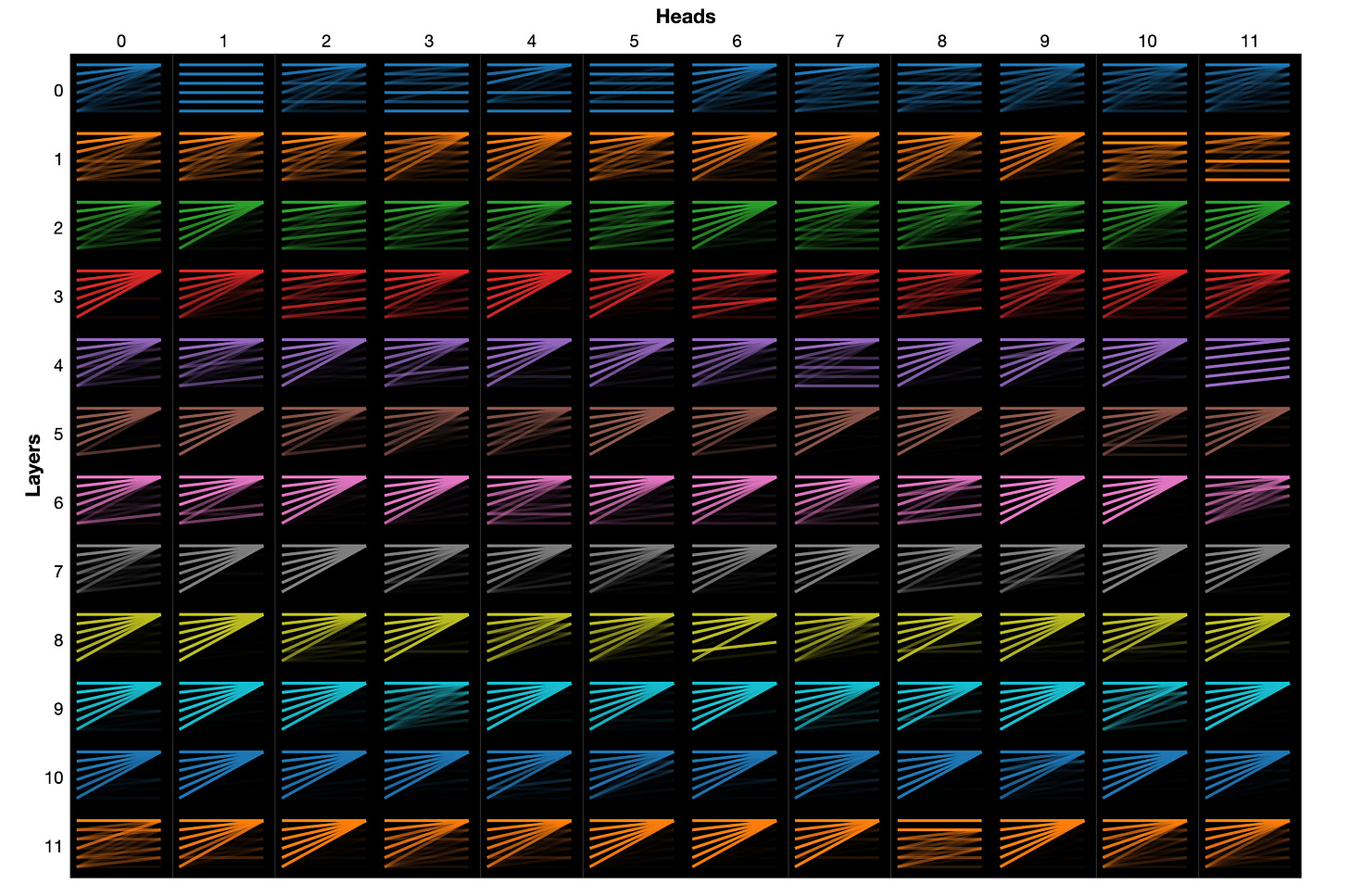
Right now, John and Jessica. The top 2 images show the output for a single attention head and single token. The bottom graphic shows the attention pattern for all 144 attention heads in GPT-2.Here’s another really nice visualization of a toy 2-layer model by Anthropic that I couldn’t figure out how to embed. You can also play around a bit with attention head visualization in the supplementary Colab notebook as well.
We’ll just work through a toy model with a single attention head.
Two Separate Algorithms
A given attention head does two main things. One part is figuring out which previous words to attend to, which we’ll call the attention side of the algorithm. The other part is figuring out what information to move from a previous word (the source) to the current word (the destination) given that the source is attended to, which we’ll call the value side of the algorithm. These are two totally separable parts of the attention process which vary independently of one another, and we can look at each in isolation from the other.
The Attention Side
Let’s start with the attention side. It’s more intuitive than the value side in one sense. For each token, the attention pattern is just a probability distribution over itself and previous tokens, where the “probability” assigned represents how much attention is paid. This is very easy to interpret.
On the other hand, the actual mechanics of calculating attention scores are a bit more involved. I’ll tell a standard version of the story here, although we’ll see in Part II there are other ways to think about what’s going on.
The Standard Story: Queries and Keys
As a first pass, the idea is that each token gets assigned both a query and a key by the attention head. The query encodes what kind of information that token is on the hunt for, and the key encodes what kind of information it contains.
Let’s go back to the chestnut The world is the totality of facts, not of things. In a given attention head, a word like is might be looking for a singular noun (that could serve as its subject), so its query could encode that. Each token is also assigned a key. A key is meant to encode whether a given token is a good answer to the query. So world might have a key encoding that it is a singular noun. How well is’s query matches world’s key determines how much attention is gives to world.
Quick analogy. Imagine you are given a sheet of paper with a locker combination, but you don’t know which locker the the combination works for. You’re told that when you find the right locker, there will be something you’ll deeply value inside. The sheet of paper is like the query that you test against each locker (the key), and what’s inside is the value you want to take.
Toy Model: Queries and Keys
Let’s just dive straight into the toy model with the string Amy saw Will for this one. We’ll concoct a single attention head. Last we saw, we represented the string like this:
Each word currently gets represented with four dimensions—four different numbers encoding properties it has.
Our concocted attention head will only pay attention to the first two features: Future and Tool. And the queries and keys for each word will likewise only have two numbers associated with them.
The attention head contains its own instructions for how to generate each word’s query and key. Let’s stipulate that the first number for the a word’s query adds together its Future and Tool score. And the second number is just identical to its Tool score.
(Now, this is a toy model, so I’m just stipulating how the queries and keys work for the sake of making things as concrete as possible. There’s no deep reason behind these choices.)
This means we end up with the following queries for this attention head.
The attention head also tells us how to make keys. We’ll stipulate that the first number for a word’s key will be its Tool score, and the second number will be the sum of its Future and Tool scores.
This means we end up with the following keys for this attention head.
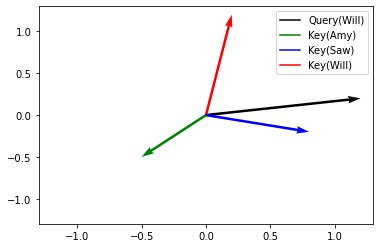
We now check each word’s query against each word’s key. To get a sense for how this works, look at the graph below that shows Will’s query against the keys for Amy, saw, and Will.
The most important factor is the angle between the query and the keys. We see that the angle between Will’s query and saw’s key is the smallest, and the angle between Will’s query and Amy’s key is the largest. This means that Will will give the most attention to saw and the least attention to Amy.4
To actually calculate how well Will's query matches various keys, we just take dot product between the key and the query vectors. In more detail, to calculate the initial attention score Will gives to saw, we take Will’s query vector [1.2, .2] and saw’s key vector [.8, -.2]. We multiply each of the coordinates and add together. So we get 1.2×.8 + .2×(-.2) = .92 as the initial attention score.
If we do this for all queries against all keys, we end up with the following unnormalized scores:
The rows represent an unnormalized version of how much attention each token is paying to each token. So Will gives -.7 to Amy, .92 to saw, and .48 to itself. Bigger numbers represent more attention.
There are two problems. First, each row is suppose to be a probability. So all numbers should be between 0 and 1 and add up to 1. Second, the model should only allow a token to pay attention to itself and previous tokens. When making predictions about what the next token is, it shouldn’t be able to see the future first. So, Amy shouldn’t be allowed to attend to saw or to Will, and saw shouldn’t be allowed to attend to Will. Will, on the other hand, should be allowed to attend to Amy, saw, and Will.
Some Mathy Details You Can Skip if You Want
The way we convert rows to probabilities is with a function called softmax. The details aren’t too important (aside from the fact that this function is non-linear), but here they are. To calculate the attention Will gives to saw, we take:
The denominator is just the sum e^i for each entry i in Will’s row. The numerator, here, is the initial score that Will gives to saw. If we wanted to calculate the attention Will gives to Amy, the numerator would be e^(-.7) instead.
If we take the softmax for each row, we now have probabilities. Here they are rounded to two decimal places.
So, Will gives 11% of its attention to Amy, 54% to saw, and 35% to itself.
However, we still have the illicit attention to the future, so we have to zero those probabilities out and renormalize. I’ll skip a prolonged explanation.
Attention Pattern
We end up with:
All right, that’s it! We now have our attention pattern for this head. I’ll return to attention at the end of this section, but let’s now work through how value works.
The Value Side
The value side of the algorithm determines what information to move if asked. The easiest way to understand this is when one token gives 100% of its attention to another.
Suppose in Right now, John and Jessica, the attention head has Jessica attend solely to and. The value for and might represent some information that, when moved over to Jessica, allows the model to predict a plural verb instead of a singular one.
Going back to our earlier analogy: the attention side tells you which locker to open, and the value is what’s in the locker.
Toy Model: Value
Value is a bit harder to interpret, since an attention head can encode all sorts of information for a token, and it will generally be harder for humans to read off what the meaning of this information is. However, the actual mechanics are relatively easy to understand.
As with queries and keys, the attention head comes with instructions for how to turn the original embedding into values. We’ll again have value be two dimensional. This time, let’s make things even easier on ourselves and have the first coordinate of value for a token just be the Future score, and the second coordinate just be the Tool Score.
Our embedding is currently:
So this means we end up with:
Well, that wasn’t so bad.
Putting Attention and Value Together
So now we have attention scores and values. We now use the attention scores to figure out how much of the value to move over.
From our attention pattern, we have Will giving 11% of its attention to Amy, 54% of its attention to saw, and 35% to itself. So, it will take 11% of Amy’s value, 54% of saw’s value, and 35% of Will’s value and add that together. Written out, this is:
If we do this for each row, we get:
Now, we’ve done the hard work of computing attention and value and putting those together. But our result only has two dimensions, and our original embedding had four. We want the output of the attention head to change our original embedding. So, we have to take the result and make it four dimensional somehow and add it back.
The attention head also has instructions for how to do this. We’ll make it really easy on ourselves and just stipulate that it adds two zeros onto the end of each row as follows:
Finally, we take the output and just add it back into the original embedding. This is just done coordinate by coordinate. So, saw’s initial embedding had a Future score of -1, and the attention head has its first output as -.49, so it’s new Future score will be -1.49.
We end up with our new embedding of:
So, we see that after attention, the model is less inclined to think of Will as a future indicator and has at least changed a bit in its view of whether saw is a tool or a past indicator.
And that’s how attention works.
A Few Remarks and Takeaways on Attention
We’ll talk more about attention in Part II, but I want to get a few points across here.
To recap: The attention side determines what to pay attention to, and the value-side determines what information to move from token to token. This is the only way information moves around from one token to another in a string.
The attention head both decides what the tokens in the string should pay attention to and what information is associated with each token if attended to (i.e., its value).
The attention head has four different sets of instructions. The first is the instructions for changing an embedding into queries, the second is the instructions for changing an embedding into keys, the third is the instructions for changing an embedding into values, and the last is the instructions for changing the result of the attention process into an output that gets added onto the initial embedding.
For a given head, these instructions stay the same no matter what embedding it sees. So, the embeddings change from string to string, but the instructions belong to the head.
The instructions also all have to be relatively simple. If you haven’t had any linear algebra, think of it like this. The first coordinate for the query, for example, could have said something like: add all the coordinates of the embedding together. Or it could be: take the first coordinate of the embedding and multiply it by -18 and add that to the rest of the coordinates. You get to multiply coordinates by fixed numbers and add them together. You can’t do fancy things like take the square root of the first coordinate, though, because that can’t be expressed as multiplying the first coordinate by a fixed amount regardless of its value.
If you have had linear algebra: the instructions are encoded as matrices Q, K, V, and O. And you just multiply the embedding by Q, K, and V to get the queries, keys, and values for the string. You multiply the result by O to get the output of the attention head that gets added back onto the embedding. All of this is completely linear. The only non-linear part is in generating the attention scores, where you have to take a softmax.
MLPs
Ok, we’re almost there. The last main portion of the architecture is the one I’ll spend the least time on, and it’s one I don’t think you should worry too much about if this is your first encounter with transformers. This portion is also the least understood, in that we have less of an understanding of what it accomplishes in a layer.
After we’ve added the outputs of the attention heads onto our original embedding, we pass the new vectors representing the tokens in our original string through something called a multi-layer perceptron (MLP). We do this in parallel. Each vector (corresponding to a token in the original input) goes through this network on its own. No information is moved from token to token.
Now, why do we have MLPs in addition to attention heads? The basic reason is that attention heads are nearly linear.5 When calculating attention scores, you do something not quite linear when you normalize the unprocessed scores into probabilities. But aside from that one tiny step, everything else is just rotations and stretching.
When you put a bunch of linear functions together, you get a linear function. So we’re going to want a bit more non-linearity somehow. As far as I can tell, this basically is about as much as we understand currently for why we have MLPs thrown into the mix.
Basic Idea of MLPs
The very brief summary of the idea is as follows: you take our massaged vector corresponding to a word in the string (4 dimensions for the toy model, 768 for GPT-3 Small). You then set up a bunch of different nodes, which we’ll call neurons. (In practice, there are usually 4 times as many neurons as the number of dimensions.)
Each neuron computes a value based on the values of each of components in the vector. And then we use the values of the neurons to generate a final output.
Again, I think a worked example is the best place to start.
Toy Model: MLP
We have a four dimensional embedding, so in this super small model, we’d normally set up a 16 neuron network. But that’s a bit of a pain to do by hand, so we’ll just use one neuron.
Our current embedding (post attention) is:
For the input to our neuron, we again have a set of simple instructions. We’ll stipulate the instructions are: Multiply the Future score by -1, and add it to the Tool score and the Fame score. We end up with a single number as input to this neuron. In this case, we have:
We now do something slightly non-linear.6 We’ll follow the original Vaswani et al. paper, where the authors used the ReLU, where ReLU(x) = max(x,0). E.g., ReLU(7.2) = 7.2, ReLU(0.5) = 0.5, but ReLU(-2) = 0.7 This gets us:
Now, we need to use this computation to massage our embedding. This time, let’s just stipulate that we add the result to the Male score. (In general, there’s another set of linear instructions that come with the MLP that tells you how to use the result to massage the embedding.)
We end up with a final embedding after this layer of:
(You might notice that there was only one layer to this “multi”-layer perceptron. Rather surprisingly, this isn’t just a fact about the toy model. Even full GPT-3 has only single layer MLPs, although each layer has 49,152 neurons instead of just the one we used.)
Putting it All together
We’ve now covered the main conceptual components. We embed the initial string into meaningful vectors, one for each token. We then pass these vectors into a bunch of attention heads and add the outputs onto the original embedding. We take this new vector and run it through an MLP and add the output onto the embedding.
What’s next? Well, we have to do this a bunch of times. So, after the MLP, there’s a new set of attention heads and then a new MLP, and so on. Again, for GPT-3 Small, we do this 12 times, and for full GPT we do it 96 times. We’ll talk more about why you might need all these layers in a later post.
At the end of this, we have a potentially heavily massaged list of vectors representing each token in our string. Now, it’s time to unembed and make predictions. What we end up with is just a probability distribution over the next token.
I don’t think the mechanics are especially conceptually interesting, but we’ll run through it for the toy model for the sake of completeness.
Toy Model: Unembedding
We have our final embedding:
And we need to turn it into predictions about what the next token is. As usual, we have a simple set of instructions for taking the numbers in this matrix and transforming them into another matrix. I’ll suppress the detailed description this time. But if you recall, we had a six word vocabulary we were working with. So let’s say we end up with something like this:
We then take the softmax for each row (just like when calculating attention scores). So we end up with the following predictions:
So this means that, if fed just the string Amy, the model predicts that Will will be the next word with 20% probability. If fed just the string Amy saw, it predicts yesterday will be the next word with 51% probability. If fed Amy saw Will, it predicts Arnett will be the next word with 83% probability.
Conclusion
That’s the basic idea of attention heads. You embed the string token-by-token. Then you move information around and change the embedding. Then you do a bit of computation on each token’s embedding (without moving information around) with an MLP. Then you keep doing the attention/MLP thing for quite a while. Then you make predictions with an unembedding.
There’s a lot more to say. But that’s enough for right now. In the second post, I’ll do some cleanup, corrections, and conceptual commentary. And I’ll talk about training the model in the third post.
Further Reading and Resources
Colab notebooks for visualizations
Short Colab notebook for this two part series. (Basically, just showing off parts of Bertviz and Circuitsvis libraries for attention visualization.)
Neel Nanda’s exploratory visualization demo
Other transformer walkthroughs
Jay Alammar’s Illustrated Transformer
Andrej Karpathy’s YouTube walkthrough coding up a small transformer trained Shakespeare text
Anthropic’s A Mathematical Framework for Transformer Circuits. (This improved my understanding of transformers more than anything else and will be linked to multiple times in these posts.)
Neel Nanda’s helpful accompanying YouTube video
This is the most basic type of neural network and was theorized about as early as the late 40s with some workable implementations in the 1980s.
Confusingly, multi-layer perceptrons also have layers, but these are different from the layers of a transformer. If we say a transformer model has 12 layers, we mean it has 12 different attention head block + MLP blocks.
Well, not quite. You get a vector close to the vector for queen. And if you find the word in your vocab closest king - man + woman, it will be the vector for queen.
The length (i.e., magnitude) of the key and query vectors also matters. (We’re ultimately taking dot products here.) But there’s a bunch of details about normalization, etc., that I’m glossing over, so I’m focusing on the angle as a good enough proxy.
Well, technically, bilinear. But that doesn’t really help.
You might think: Hey, that really looks linear! And you’re right. It still kind of shocks me that this is enough non-linearity. But it is non-linear, and it works. (In ancient times, people used much less linear functions, but then the ReLU turned out to work better in deep learning somehow. Standard theoretical explanations for why ReLU was a big improvement don’t make sense to me.)